T-test vs Wilcoxon vs Median Test

Author

Lukas Graz

Published

September 20, 2023

Define a list of laws (i.e., distributions) with mean and sd.

nsim <- 200
library(coin)

# functions 
n <- 40 # per group
laws <- list(
  norm = function(mean=0, sd=1) mean + sd *  rnorm(n, 0, 1),
  logn = function(mean=0, sd=1) mean + sd * (rlnorm(n, sdlog=1) - 1.65) / 1.95,
  exp1 = function(mean=0, sd=1) mean + sd * (rexp(n) - 1),
  exp2 = function(mean=0, sd=1) mean + sd * (rexp(n)^2 - 2) / 3.94,
  emix = function(mean=0, sd=1) mean + sd * (c(rep(0, n/2), rexp(n/2)) - 0.5) / 0.84
)
set.seed(123)
options(digits=3)

get_data_all_laws <- function(){
  dat <- lapply(names(laws), function(fname){
    f <- laws[[fname]]
    data.frame(y=f(), fun=fname)
  }) 
  dat <- do.call(rbind, dat)
  dat
}
boxplot(y ~ fun, get_data_all_laws(), main= "Laws illustrated")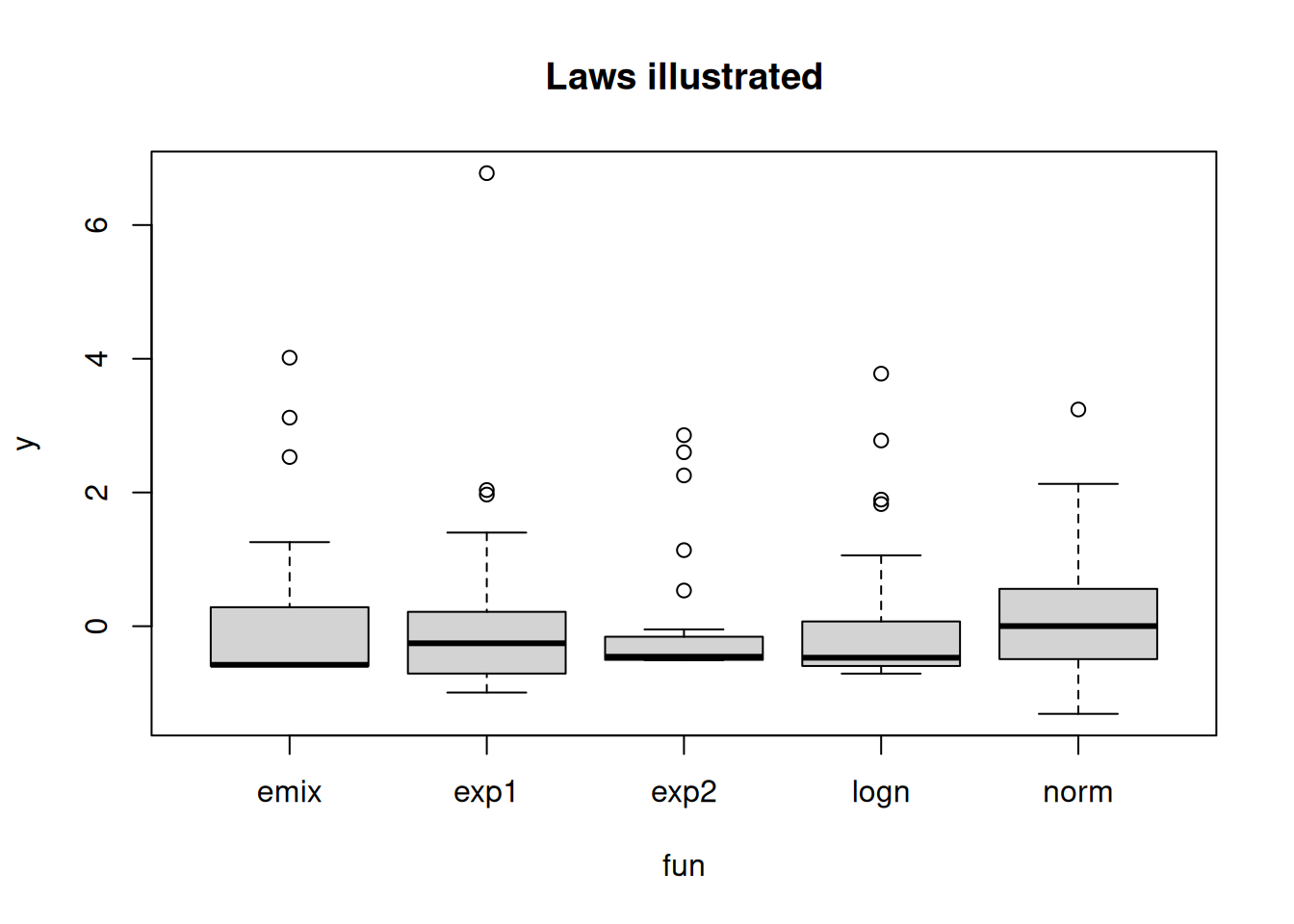

Verify mean and standard deviation

sapply(laws, function(f) mean(replicate(10000, mean(f(0, 1)))))
     norm      logn      exp1      exp2      emix 
 1.55e-03 -2.89e-03 -1.66e-03 -8.53e-05 -1.32e-03 
sapply(laws, function(f) mean(replicate(10000, mean(f(1, 2)))))
 norm  logn  exp1  exp2  emix 
1.003 1.002 0.998 0.994 0.997 
sapply(laws, function(f) mean(replicate(10000,   sd(f(0, 1)))))
 norm  logn  exp1  exp2  emix 
0.994 1.008 0.977 0.999 1.000 
sapply(laws, function(f) mean(replicate(10000,   sd(f(1, 2)))))
norm logn exp1 exp2 emix 
1.99 2.01 1.96 1.99 2.00

Define the tests used

pval_t <- function(d) t.test(y ~ group,d)$p.value
pval_w <- function(d) coin::pvalue(coin::wilcox_test(y ~ group, d))
pval_m <- function(d) coin::pvalue(coin::median_test(y ~ group, d))
# retuns data with f1() for group "A" and f2(mean2, sd2) for group "B"
get_data <- function(f1, f2, mean2=0, sd2=1){
  d <- rbind(
    data.frame(
      y=f1(),
      group="A"
    ),
    data.frame(
      y=f2(mean2, sd2),
      group="B"
    ))
  d$group <- as.factor(d$group)
  d
}

# get power of tests
get_power <- function(f1, f2, nsim=1000, mean2=0, sd2=1) {
  data_list <- replicate(nsim, get_data(f1, f2, mean2=mean2, sd2=sd2), simplify = FALSE)
  c(t = mean(sapply(data_list, pval_t) < 0.05),
    w = mean(sapply(data_list, pval_w) < 0.05),
    m = mean(sapply(data_list, pval_m) < 0.05))
}

# get all combinations of functions
fun_comb <- expand.grid(names(laws), names(laws)) |> as.matrix()
rnames <- apply(fun_comb, 1, paste0, collapse="_")

sim <- function(nsim=1000, mean2=0, sd2=1) {
  fun_comb_list <- split(fun_comb, row(fun_comb))
  coverage <- parallel::mclapply(fun_comb_list, function(f_names){
    f1 <- laws[[f_names[1]]]
    f2 <- laws[[f_names[2]]]
    get_power(f1, f2, nsim=nsim, mean2=mean2, sd2=sd2)
  })
  coverage <- do.call(rbind, coverage) 
  rownames(coverage) <- rnames
  colnames(coverage) <- paste0(
    colnames(coverage), " ", as.character(mean2), " ", as.character(sd2))
  coverage |> as.data.frame()
}

Simulation

set.seed(4321)
null <- sim(nsim=nsim)
set.seed(4321)
s_diff <- sim(nsim=nsim, sd2=2)
set.seed(4321)
s_difff <- sim(nsim=nsim, sd2=5)
set.seed(4321)
mu_diff <- sim(nsim=nsim, mean2 = 0.1)
set.seed(4321)
mu_difff <- sim(nsim=nsim, mean2 = 0.2)
results <- cbind(
  null,
  s_diff,
  s_difff,
  mu_diff,
  mu_difff
)
results * 100
          t 0 1 w 0 1 m 0 1 t 0 2 w 0 2 m 0 2 t 0 5 w 0 5 m 0 5 t 0.1 1 w 0.1 1
norm_norm   4.0   3.5   5.5   3.0   4.5   4.0   2.0   6.5   4.0     8.5     7.5
logn_norm   5.0  11.5  28.5   6.0   7.5  17.0   5.0   8.0  12.5    10.5    20.5
exp1_norm   2.5   7.0  17.0   5.0   7.5  13.5   3.0   8.0   8.5    11.0    19.5
exp2_norm   9.0  15.0  47.5   6.5   7.0  26.5   3.0   7.5  15.5    10.0    29.0
emix_norm   2.5  11.0  49.5   3.5   8.0  25.5   5.5  10.5   9.5     8.0    19.5
norm_logn   5.5  13.5  29.5   8.0  42.5  59.5  10.5  75.0  74.5     3.0     4.5
logn_logn   3.0   5.5   4.5   4.0  54.0  32.0   9.0  70.5  63.0     8.0    17.0
exp1_logn   7.0   8.0   4.5  10.0  57.5  33.0  12.0  72.0  62.0     7.0    21.0
exp2_logn   2.5   8.0   7.5   6.5  55.5  36.0  10.0  73.5  66.5     9.5    13.0
emix_logn   2.0   3.0  11.0   7.0  61.0   0.5   8.0  74.5  15.5     1.0    29.5
norm_exp1   3.5   9.0  17.5   8.5  26.0  33.5  10.5  48.5  47.5     6.5     6.0
logn_exp1   3.5   6.0   5.5   6.0  35.5  18.0   6.5  45.0  39.0     6.0     6.0
exp1_exp1   3.5   5.5   5.5   6.0  28.5  13.0   8.5  54.5  46.0     7.5    10.0
          m 0.1 1 t 0.2 1 w 0.2 1 m 0.2 1
norm_norm     3.5    15.5    14.0    10.0
logn_norm    44.5    21.5    40.5    63.0
exp1_norm    35.0    14.5    29.5    43.5
exp2_norm    64.0    18.0    43.5    76.5
emix_norm    59.0    13.0    37.5    76.5
norm_logn    12.0    11.0     8.5     9.5
logn_logn     9.0    16.5    55.0    27.0
exp1_logn     5.0    12.5    36.0    12.5
exp2_logn    21.5    19.5    47.0    56.5
emix_logn    32.5    14.0    93.5    58.5
norm_exp1    10.5    13.0     4.5     2.0
logn_exp1     9.0    12.0    18.5    16.5
exp1_exp1     8.5    14.0    35.5    17.0
 [ reached 'max' / getOption("max.print") -- omitted 12 rows ]

Confidence intervals of ratios

prop <- function(ratio, nsim){
  confint_ <- prop.test(round(ratio*nsim), nsim)$conf.int[1:2]
  names(confint_) <- c("lower", "upper")
   c( 
    ratio= ratio,
    confint_
)}
sapply(c(0:4/40, 3:10/20), prop, nsim) |> as.data.frame() * 100
        V1    V2   V3    V4    V5   V6   V7   V8   V9  V10  V11  V12  V13
ratio 0.00 2.500 5.00  7.50 10.00 15.0 20.0 25.0 30.0 35.0 40.0 45.0 50.0
lower 0.00 0.924 2.56  4.41  6.37 10.5 14.8 19.3 23.8 28.5 33.2 38.0 43.1
upper 2.35 6.056 9.27 12.30 15.23 20.9 26.4 31.7 36.9 42.1 47.2 52.2 56.9

this gives an idea of the uncertainty of a ratio given 200 simulations

redo analysis but with groupwise equal medians

Define a list of laws (i.e., distributions) with median and sd

# functions 
n <- 40 # per group
# mean == to keep notation consistent
laws <- list(
  norm = function(mean=0, sd=1) mean + sd *  rnorm(n, 0, 1)
  ,logn = function(mean=0, sd=1) mean + sd * (rlnorm(n, sdlog=1) - 1.02) / 1.95
  ,exp1 = function(mean=0, sd=1) mean + sd * (rexp(n) - 0.706)
  ,exp2 = function(mean=0, sd=1) mean + sd * (rexp(n)^2 - 0.523) / 3.94
  ,emix = function(mean=0, sd=1) mean + sd * (c(rep(0, n/2), rexp(n/2)) -0.025) / 0.84
)

verify median and standard deviation

sapply(laws, function(f) mean(replicate(10000, median(f(0, 1)))))
     norm      logn      exp1      exp2      emix 
-0.000142 -0.000216  0.002144  0.000204  0.000246 
sapply(laws, function(f) mean(replicate(10000, median(f(1, 2)))))
 norm  logn  exp1  exp2  emix 
1.000 1.001 0.998 1.000 0.999 
sapply(laws, function(f) mean(replicate(10000,     sd(f(0, 1)))))
 norm  logn  exp1  exp2  emix 
0.996 1.006 0.978 1.010 1.003 
sapply(laws, function(f) mean(replicate(10000,     sd(f(1, 2)))))
norm logn exp1 exp2 emix 
1.99 2.00 1.95 1.99 2.01 
boxplot(y ~ fun, get_data_all_laws(), main= "Equal Medians (in expectation)")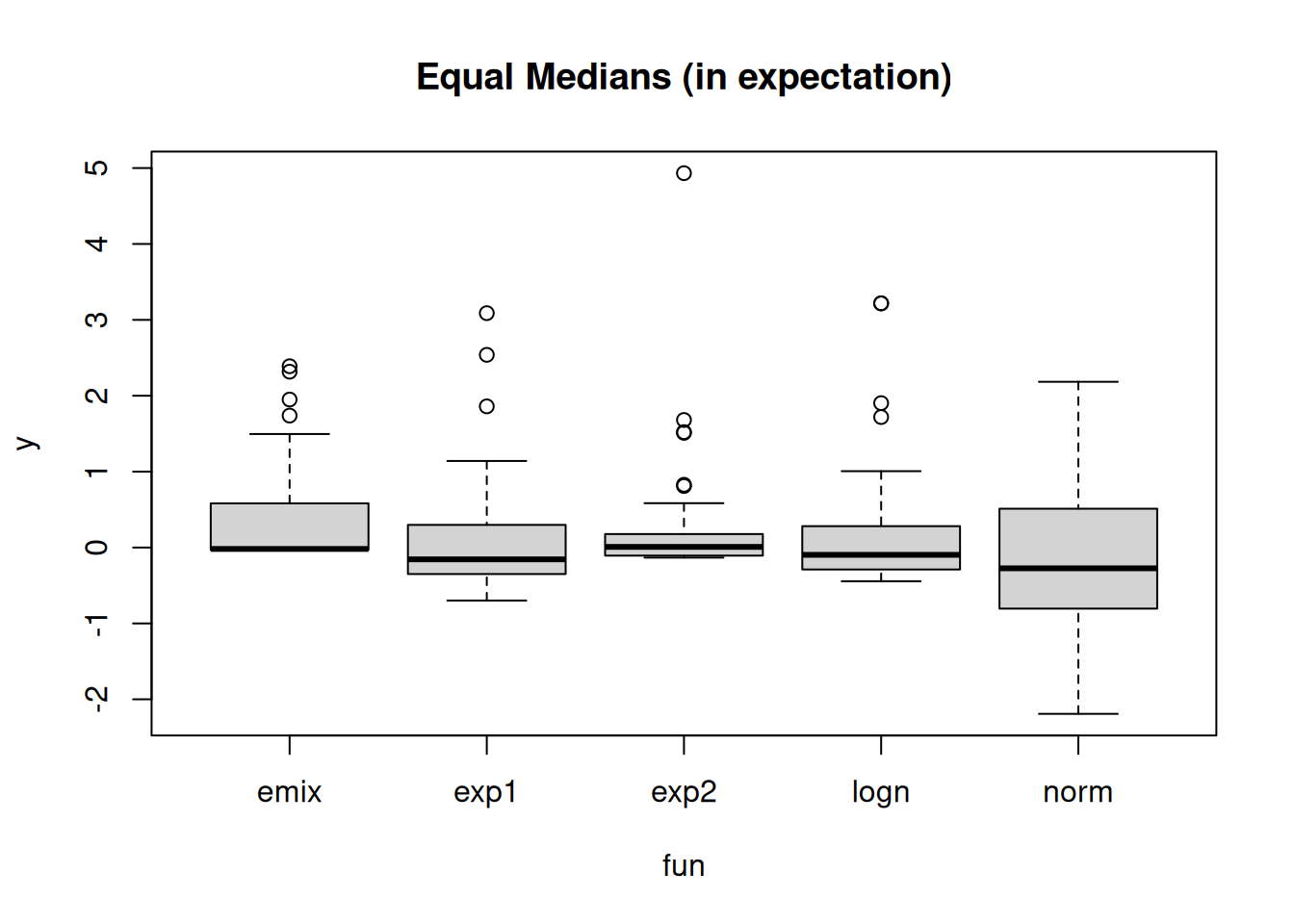

set.seed(4321)
null_median <- sim(nsim=nsim)
set.seed(4321)
s_diff_median <- sim(nsim=nsim, sd2=2)
set.seed(4321)
s_difff_median <- sim(nsim=nsim, sd2=5)
set.seed(4321)
mu_diff_median <- sim(nsim=nsim, mean2 = 0.1)
set.seed(4321)
mu_difff_median <- sim(nsim=nsim, mean2 = 0.2)
results_median <- cbind(
  null_median,
  s_diff_median,
  s_difff_median,
  mu_diff_median,
  mu_difff_median
)  
results_median * 100
          t 0 1 w 0 1 m 0 1 t 0 2 w 0 2 m 0 2 t 0 5 w 0 5 m 0 5 t 0.1 1 w 0.1 1
norm_norm   2.0   2.0   2.5   5.0   6.5   5.5   9.5  11.5  11.5     7.5     7.0
logn_norm  26.0  16.0   5.0  11.5  16.5  11.0   5.0   8.5   9.0    14.0     8.0
exp1_norm  21.5  10.5   6.5  13.0  12.0   8.0   3.0   6.0   8.5    10.5     6.5
exp2_norm  27.5  19.5   7.0  18.0  17.0  10.5   5.5  10.0  13.5    18.5    12.0
emix_norm  75.0  53.0   1.0  30.5  27.5   2.5  12.0  15.5   4.5    55.5    35.5
norm_logn  22.5  11.0   6.0  34.5  13.0   3.5  43.0   9.0   7.5    33.5    27.5
logn_logn   3.5   5.5   3.5   7.0   7.5   6.0  23.5  11.5  10.0     6.5    15.5
exp1_logn   6.0   9.0   6.5  15.5   8.0   5.5  25.5  10.5   8.0     7.5    20.5
exp2_logn   3.0  16.5   5.5   4.5  14.5   6.5  21.5  14.5  11.5     6.0     3.5
emix_logn  26.5  64.5   0.0   4.5  33.0   0.5  17.0  17.0   1.0     9.0    25.0
norm_exp1  27.0  14.5   8.5  39.5   9.0   3.5  46.5  10.0  14.5    44.5    30.0
logn_exp1   4.0   8.0   4.0  13.0  16.5  10.5  21.5  10.5  13.5     8.5     6.0
exp1_exp1   2.5   3.0   5.5  16.0   7.5   8.5  26.5   9.5   7.5     7.0     9.5
          m 0.1 1 t 0.2 1 w 0.2 1 m 0.2 1
norm_norm     6.5    12.5    11.5    11.0
logn_norm     6.0     6.5     8.5    11.5
exp1_norm     7.5     7.5     6.5    13.0
exp2_norm     7.5     5.0     5.0    20.5
emix_norm     3.5    34.0    16.5     3.0
norm_logn    10.0    64.5    53.5    17.5
logn_logn     9.5    16.0    51.0    24.5
exp1_logn     9.0    15.5    50.0    24.5
exp2_logn    17.5    13.0    24.0    37.0
emix_logn     1.0     2.5     1.0     3.0
norm_exp1     8.5    57.0    41.5    13.0
logn_exp1     7.5    10.5    13.5    13.5
exp1_exp1     5.0    17.0    30.0    15.5
 [ reached 'max' / getOption("max.print") -- omitted 12 rows ]