Back to Article
Predict RL via HM
Download Source

Predict RL via HM

Author

Lukas Graz

Published

July 10, 2025

Setup + Preprocessing

In [1]:
suppressPackageStartupMessages({
  library(dplyr)
  library(ggplot2)
  library(egg)
  library(kernlab)
  library(mgcv)  # for GAM models - smoothing
  library(gridExtra)  # for combining plots
  library(tidyr)  # for pivoting data
})
Warning: package 'kernlab' was built under R version 4.5.1
theme_set(theme_minimal())

options(digits = 3)
source("R/data_prep.R")
Number of matches per filter criteria (not disjoint)
  Headphone  PRS_all_NA    Distance Activity_NA    Duration  HMNoise_NA 
        303         226         221         102          96          96 
JourneyTime 
         20 
Keep  1494 of 2206 observations
Warning: package 'missForest' was built under R version 4.5.1
Imputing PRS_orig_vars
In [2]:
Code 
D$RL_NDVI     <- pmax(0, D$RL_NDVI)
D_trn$RL_NDVI <- pmax(0, D_trn$RL_NDVI)
D_tst$RL_NDVI <- pmax(0, D_tst$RL_NDVI)

D$LANG <- as.factor(D$LANG)
D_trn$LANG <- as.factor(D_trn$LANG)
D_tst$LANG <- as.factor(D_tst$LANG)

D$SEX <- as.factor(D$SEX)
D_trn$SEX <- as.factor(D_trn$SEX)
D_tst$SEX <- as.factor(D_tst$SEX)

D$JNYTIME <- D$JNYTIME + quantile(D$JNYTIME[D$JNYTIME > 0], 0.05, na.rm=TRUE)/2
D_trn$JNYTIME <- D_trn$JNYTIME + quantile(D_trn$JNYTIME[D_trn$JNYTIME > 0], 0.05, na.rm=TRUE)/2
D_tst$JNYTIME <- D_tst$JNYTIME + quantile(D_tst$JNYTIME[D_tst$JNYTIME > 0], 0.05, na.rm=TRUE)/2

D$DISTKM <- D$DISTKM + quantile(D$DISTKM[D$DISTKM > 0], 0.05, na.rm=TRUE)/2
D_trn$DISTKM <- D_trn$DISTKM + quantile(D_trn$DISTKM[D_trn$DISTKM > 0], 0.05, na.rm=TRUE)/2
D_tst$DISTKM <- D_tst$DISTKM + quantile(D_tst$DISTKM[D_tst$DISTKM > 0], 0.05, na.rm=TRUE)/2


D$SPEED_log <- log(D$DISTKM / D$JNYTIME)
D_trn$SPEED_log <- log(D_trn$DISTKM / D_trn$JNYTIME)
D_tst$SPEED_log <- log(D_tst$DISTKM / D_tst$JNYTIME)


# logical_vars <- c("ALONE","WITH_DOG","WITH_KID","WITH_PAR","WITH_PNT","WITH_FND")
# D[logical_vars] <- lapply(D[logical_vars], as.numeric)
# D_trn[logical_vars] <- lapply(D_trn[logical_vars], as.numeric)
# D_tst[logical_vars] <- lapply(D_tst[logical_vars], as.numeric)
In [3]:
Train/test split 
nams <- names(D)
nams[grep("HM|RL", nams)]
 [1] "HM_NOISELVL" "HM_NDVI"     "HM_NOISE"    "RL_NDVI"     "RL_NOISE"   
 [6] "HM_COORDX"   "HM_COORDY"   "RL_COORDX"   "RL_COORDY"   "RL_GCOORD"  
[11] "RL_GCOORDN"  "RL_GCOORDW"
Train/test split 
vars <- c(
  # "HM_NOISELVL",
  # "HM_COORDX","HM_COORDY","RL_COORDX","RL_COORDY","RL_GCOORD",
  # "RL_GCOORDN","RL_GCOORDW",
  "HM_NDVI","HM_NOISE","RL_NDVI","RL_NOISE",
  "ALONE","WITH_DOG","WITH_KID",
  "WITH_PAR","WITH_PNT","WITH_FND",
  "LANG", # "AGE","SEX",
  "DISTKM_sqrt", "JNYTIME_sqrt", "SPEED_log"
) 

D_trn <- D_trn[vars]
D_tst <- D_tst[vars]

D_trn <- D_trn[complete.cases(D_trn), ]
D_tst <- D_tst[complete.cases(D_tst), ]

D_trn[] <- lapply(D_trn[], \(x) if (is.numeric(x)) scale(x) else x)
D_tst[] <- lapply(D_tst[], \(x) if (is.numeric(x)) scale(x) else x)

# summary(D[vars])
In [4]:
cor(cbind(D_trn[c("DISTKM_sqrt", "JNYTIME_sqrt", "SPEED_log")]))
             DISTKM_sqrt JNYTIME_sqrt SPEED_log
DISTKM_sqrt        1.000        0.473     0.713
JNYTIME_sqrt       0.473        1.000    -0.101
SPEED_log          0.713       -0.101     1.000

Remove DIST_sqrt, as it is highly correlated with the other two.

RL_NDVI

In [5]:
lm_ndvi <- lm(RL_NDVI ~ (HM_NDVI + HM_NOISE + 
  #  ALONE + WITH_DOG + WITH_KID + WITH_PAR + WITH_PNT + WITH_FND +
   LANG + # AGE + SEX +
   SPEED_log + JNYTIME_sqrt)^2, D_trn)
step_ndvi <- step(lm_ndvi, trace = FALSE, k = log(nrow(D_trn)))
summary(fit <- lm(formula(step_ndvi), D_tst))

Call:
lm(formula = formula(step_ndvi), data = D_tst)

Residuals:
   Min     1Q Median     3Q    Max 
-3.347 -0.426  0.178  0.682  1.874 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)             -0.2041     0.0859   -2.37   0.0179 *  
HM_NDVI                  0.1572     0.0386    4.07  5.4e-05 ***
LANGGerman               0.2689     0.0972    2.77   0.0058 ** 
LANGItalian             -0.0768     0.1825   -0.42   0.6740    
SPEED_log               -0.1112     0.0416   -2.67   0.0077 ** 
JNYTIME_sqrt             0.1059     0.0406    2.61   0.0094 ** 
HM_NDVI:SPEED_log       -0.1619     0.0399   -4.05  5.7e-05 ***
HM_NDVI:JNYTIME_sqrt    -0.1194     0.0395   -3.02   0.0026 ** 
SPEED_log:JNYTIME_sqrt  -0.0854     0.0394   -2.16   0.0308 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.951 on 601 degrees of freedom
Multiple R-squared:  0.108, Adjusted R-squared:  0.0963 
F-statistic: 9.11 on 8 and 601 DF,  p-value: 7.29e-12
  • R² = 0.08
  • Higher HM_NDVI corresponds to slightly higher RL-NDVI
  • higher JNYTIME_sqrt corresponds to slightly higher RL-NDVI
  • The faster (or further) you travel to RL, the more the RL_NDVI differs from HM_NDVI (negative interaction effect)
In [6]:
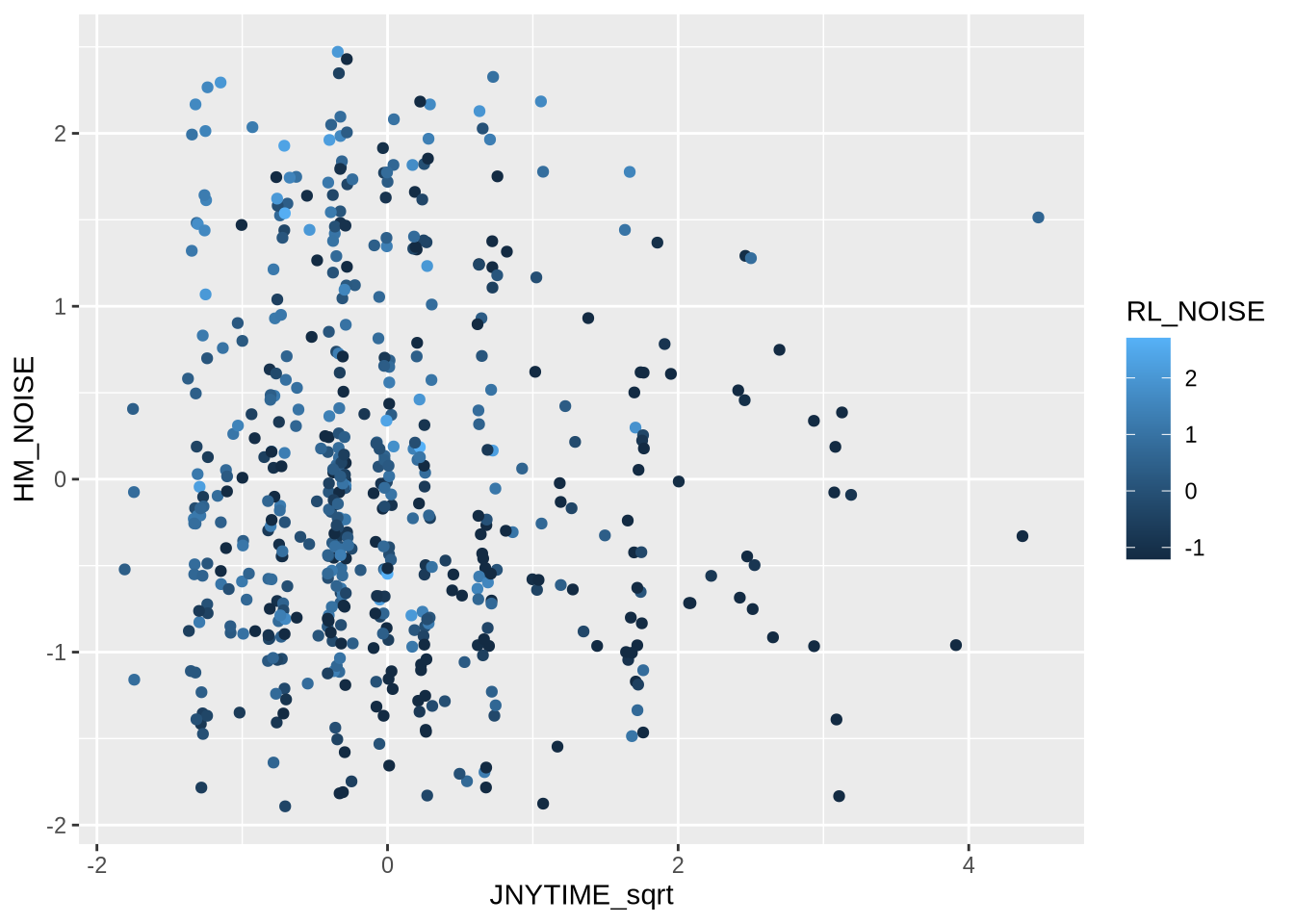
ggplot(D_tst, aes(x = JNYTIME_sqrt, y=HM_NOISE, col = RL_NOISE)) +
  geom_jitter(width=0.07, height = 0.1)

RL_NOISE

In [7]:
lm_noise <- lm(RL_NOISE ~ (HM_NDVI + HM_NOISE + 
  #  ALONE + WITH_DOG + WITH_KID + WITH_PAR + WITH_PNT + WITH_FND +
   LANG + # AGE + SEX +
   SPEED_log + JNYTIME_sqrt)^2, D_trn)
step_noise <- step(lm_noise, trace = FALSE, k = log(nrow(D_trn)))
summary(lm(formula(step_noise), D_tst))

Call:
lm(formula = formula(step_noise), data = D_tst)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.9524 -0.7719 -0.0133  0.6588  2.8255 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)           -0.000822   0.037211   -0.02    0.982    
HM_NOISE               0.240824   0.037282    6.46  2.2e-10 ***
SPEED_log             -0.065753   0.037374   -1.76    0.079 .  
JNYTIME_sqrt          -0.314663   0.037380   -8.42  2.8e-16 ***
HM_NOISE:JNYTIME_sqrt -0.037327   0.036309   -1.03    0.304    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.919 on 605 degrees of freedom
Multiple R-squared:  0.161, Adjusted R-squared:  0.156 
F-statistic: 29.1 on 4 and 605 DF,  p-value: <2e-16
  • R² = 0.184
  • Participants can’t completely escape HM_NOISE (HM_NOISE positive predictor)
  • LANGItalians have it louder (than LANG de/fr)
  • Longer JNYTIME_sqrt leads to lower NOISE
In [8]:
Fit Gaussian Process for smooth plot 

# Fit Gaussian Process
X <- as.matrix(D_tst[, c("JNYTIME_sqrt", "HM_NOISE")])
y <- D_tst$RL_NOISE

# Fit GP with RBF kernel
gp_model <- gausspr(X, y, kernel = "rbfdot", kpar = "automatic")
Using automatic sigma estimation (sigest) for RBF or laplace kernel
Fit Gaussian Process for smooth plot 

# Create prediction grid
x_range <- range(D_tst$JNYTIME_sqrt)
y_range <- range(D_tst$HM_NOISE)
grid <- expand.grid(
  JNYTIME_sqrt = seq(x_range[1], x_range[2], length.out = 50),
  HM_NOISE = seq(y_range[1], y_range[2], length.out = 50)
)

# Predict on grid
grid$predicted_RL_NOISE <- predict(gp_model, as.matrix(grid[, 1:2]))

# Get combined range for both scales
combined_range <- range(c(D_tst$RL_NOISE, grid$predicted_RL_NOISE))
In [9]:
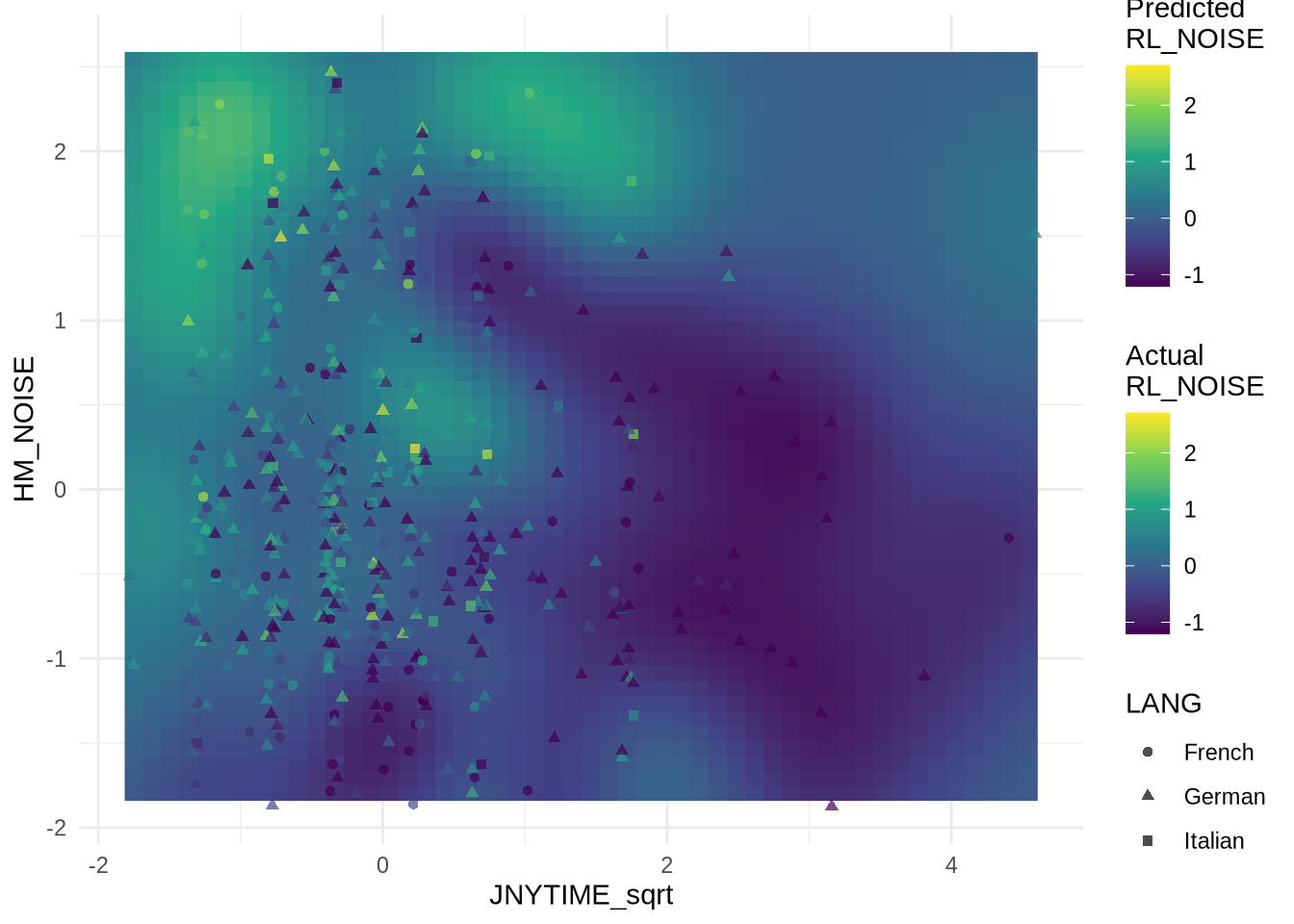
Plot predicted RL_NOISE with GP 

# Plot with matching color scales
ggplot() +
  geom_raster(data = grid, aes(x = JNYTIME_sqrt, y = HM_NOISE, fill = predicted_RL_NOISE)) +
  geom_jitter(data = D_tst, aes(x = JNYTIME_sqrt, y = HM_NOISE, col = RL_NOISE, shape = LANG), 
              width = 0.07, height = 0.1, alpha = 0.7) +
  scale_fill_viridis_c(name = "Predicted\nRL_NOISE", limits = combined_range) +
  scale_color_viridis_c(name = "Actual\nRL_NOISE", limits = combined_range) 
In [10]:
D$PRS <- rowMeans(cbind(D$FA,D$BA,D$EC,D$ES))
summary_fun <- function(x) c(mean = mean(x, na.rm = TRUE), 
                              sd = sd(x, na.rm = TRUE), 
                              median = median(x, na.rm = TRUE))

aggregate(PRS~ HM_NOISELVL, D, summary_fun)
  HM_NOISELVL PRS.mean PRS.sd PRS.median
1           1    4.989  0.886      5.000
2           2    4.928  0.915      4.917
3           3    4.857  0.926      4.833
aggregate(FA ~ HM_NOISELVL, D, summary_fun)
  HM_NOISELVL FA.mean FA.sd FA.median
1           1    5.25  1.10      5.33
2           2    5.16  1.21      5.21
3           3    5.18  1.13      5.33
aggregate(BA ~ HM_NOISELVL, D, summary_fun)
  HM_NOISELVL BA.mean BA.sd BA.median
1           1    5.11  1.20      5.00
2           2    5.04  1.17      5.00
3           3    4.95  1.20      5.00
aggregate(EC ~ HM_NOISELVL, D, summary_fun)
  HM_NOISELVL EC.mean EC.sd EC.median
1           1    4.53  1.31      4.33
2           2    4.48  1.34      4.33
3           3    4.47  1.29      4.33
aggregate(ES ~ HM_NOISELVL, D, summary_fun)
  HM_NOISELVL ES.mean ES.sd ES.median
1           1    5.07  1.42      5.19
2           2    5.04  1.38      5.00
3           3    4.83  1.55      5.00